Fascinacija složenošću bioloških oblika, posebno oblika listova različitih biljaka, intrigira čovečanstvo decenijama. Pitanje zašto biljke imaju različite oblike listova i kako se ti oblici menjaju tokom vremena i prostora postavlja se kao ključno u istraživanju kvantitativnih pristupa morfološkoj raznolikosti listova biljaka.
Dosadašnji pristupi kvantifikaciji oblika listova, bazirani na euklidskim oblicima poput krugova ili trouglova, bili su ograničeni na određene biljne vrste. Međutim, istraživači su otišli korak dalje i koristili inovativan teorijski pristup, primenjujući Bekenštajn-Hokingovu formulaciju entropije crne rupe, kako bi kvantifikovali složenost oblika listova.
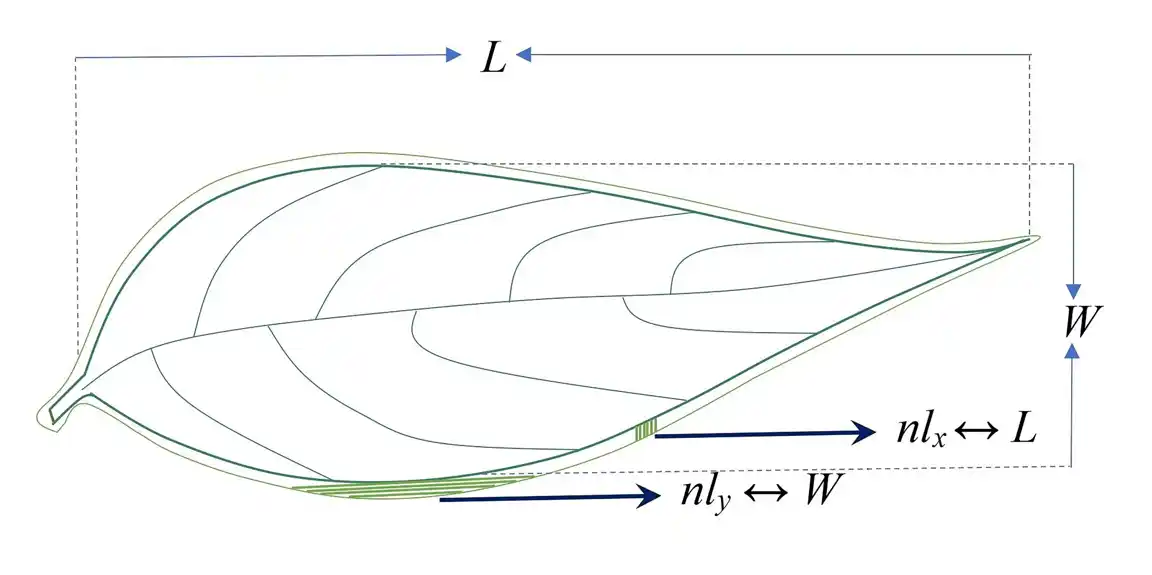
Proučavajući difuzne interfejse list-okruženje, istraživači su razvili geometrijsku entropiju kao inherentnu meru složenosti, nadmašujući druge morfometrijske tehnike. Ovaj teoretski pristup, baziran na kontinuiranom 2D proširenju Hevisajdove funkcije i funkciji faznog polja, omogućio je bolje razumevanje realnosti oblika listova.
Geometrijska entropija se pokazala proporcionalnom perimetru lista i kvadratnom korenu površine, pružajući precizniju kvantifikaciju oblika listova. Iako može sadržavati male nesavršenosti, ova metoda otvara vrata za potencijalnu klasifikaciju oblika listova na nivou roda, inspirišući biljne biologe da istraže njenu primenu u taksonomiji.
Ova istraživanja doprinose razumevanju složenosti oblika listova biljaka, a geometrijska entropija može postati ključan alat u proučavanju morfološke raznolikosti i adaptivne stabilnosti. Očekuje se da će ova nova perspektiva stimulisati dalje istraživanje u dizajnu veštačkih listova, s ciljem genetski konstruisanja optimalnih oblika listova u budućnosti.