Obično, kada razmišljamo o objektu koji se kotrlja, imamo tendenciju da zamislimo torus (kao točak bicikla) ili sferu (poput teniske loptice) koja će uvek pratiti pravu putanju kada se kotrlja. Međutim, svet matematike i nauke je uvek otvoren za istraživanje novih ideja i koncepata. Zbog toga su istraživači proučavali oblike, poput oloida, sferikona i drugih, koji se ne kotrljaju u ravnim linijama.
Svi ovi fanki oblici su zaista zanimljivi istraživačima jer nam mogu pokazati nove načine da glatko i efikasno pomeramo objekte. Na primer, zamislite da smanjite energiju potrebnu da se robot igračka pomeri ili da temeljnije mešate sastojke sa kašikom jedinstvenog izgleda. Iako su ovi neobični oblici ranije proučavani, naučnici su sada otišli korak dalje.
Zamislite igru u kojoj crtate putanju na nagnutom stolu—slično naginjanju stola za fliper da bi lopta krenula u određenom pravcu. Sada pokušajte da smislite 3D objekat koji će se, kada se postavi na vrh stola, otkotrljati nadole i tačno pratiti tu putanju, umesto da ide pravo dole. Postoji još nekoliko pravila ove igre: sto treba da bude blago nagnut (i ne previše), ne bi trebalo da bude klizanja tokom kotrljanja, a početna orijentacija objekta se može izabrati prilikom pokretanja. Osim toga, put koji crtate nikada ne sme da ide uzbrdo i mora biti periodičan. Takođe se mora sastojati od identičnih segmenata koji se ponavljaju—nešto kao u obrascima muzičkog ritma.
Međunarodni tim istraživača povezanih sa UNIST-om razmišljao je da li je moguće pronaći pobedničku strategiju za ovu igru. Želeli su da znaju da li bi, za bilo koju putanju koja se ponavlja, bilo moguće dizajnirati oblik koji se može kotrljati da bi sam pratio ovu putanju. Cilj je bio da se razvije opšti recept koji bi funkcionisao ne samo za jednostavne krivine, već i za komplikovane i isprepletene putanje. Objekti čudnog oblika stvoreni za ovu svrhu nazvani su „trajektoidi“.
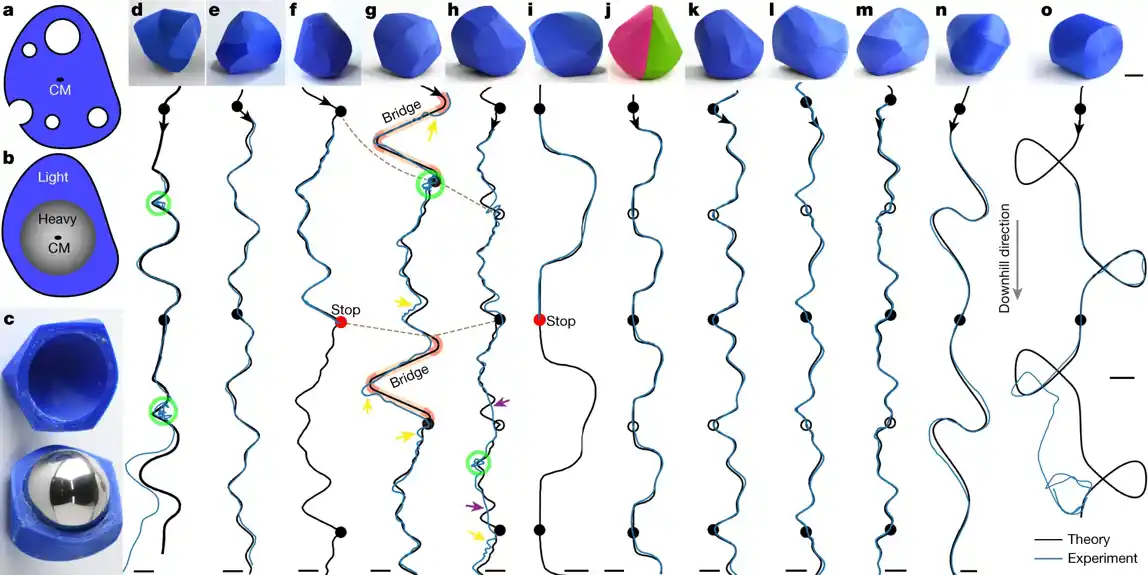
Na prvi pogled, čini se da je nemoguće da 3D objekat automatski prati unapred određenu putanju kretanja dok se kreće po svim uglovima i krivinama. Međutim, naučnici su počeli tako što su pojednostavili problem. Zamislili su da počnu sa savršeno glatkom košarkaškom loptom prekrivenom fleksibilnim materijalom koji se može rezati, nalik glini. Strateškim uklanjanjem delova materijala za pokrivanje košarkaške lopte koji su bili u kontaktu sa stolom, a istovremeno osiguravajući da sama košarkaška lopta uvek dodiruje putanju, moguće je postepeno oblikovati objekat u prilagođeni oblik. Ovaj rezultujući oblik bi onda magično pratio isti put kada se kotrlja nezavisno. Primenjujući ovaj koncept, naučnici su uspešno osmislili novu metodu za stvaranje trajektoida.
Ovi trajektoidi nisu samo teoretski; istraživači su ih 3D štampali i sproveli uspešne eksperimente. Čak su se usuđivali da naprave trajektoide koji se povremeno kreću uzbrdo ili prate staze koje se same ukrštaju. Možete čak i sami da isprobate novi algoritam za bilo koju putanju koju želite, jer su istraživači objavili onlajn alat za generisanje datoteka spremnih za 3D štampanje za trajektoide. Kredit: Priroda (2023). DOI: 10.1038/s41586-023-06306-i
Da bi trajektoid bio uspešan, mora da prati periodični put neograničeno, održavajući istu orijentaciju svaki put kada završi određeni broj perioda. Ključni aspekt je koliko perioda putanje trajektoid završava jednom „punom revolucijom“, čime se vraća njegova orijentacija. Malo je verovatno da će se stvoriti putanja koja završava jednu revoluciju za svaki period putanje. Ali s druge strane, istraživači su pokazali da je projektovanje putanje koji završava dva perioda puta za svaku revoluciju skoro uvek moguće.
Ovo svojstvo dva perioda po revoluciji je manifestacija zadivljujuće opšte osobine rotacija u 3D prostoru i može se koristiti u mnogim oblastima nauke gde se fenomeni mogu matematički opisati kao 3D rotacije—na primer, u kvantnom računarstvu, kvantnoj optici , i klasična optika.
U kvantnoj fizici postoji koncept koji se zove „Blohova sfera“, koji se koristi za opisivanje kvantnih stanja. Ova stanja obuhvataju sve moguće situacije u kojima kvantni sistem, kao što je kvantni bit ili kubit, može biti. Baš kao što sfera koja se kotrlja duž putanje pruža informacije o svom kretanju u određenim tačkama i orijentacijama, Blohova sfera predstavlja jedinstvena stanja kubita , pri čemu promene u ovim stanjima odražavaju kretanje sfere koja se kotrlja.
S obzirom na ovu matematičku sličnost, naučnici mogu da koriste isti algoritam za dizajniranje trajektoida kako bi pomogli u verifikaciji tačnosti kvantnih računara. Naučnici često procenjuju ovu tačnost ispitujući koliko se tačno tačka na Bloh sferi vraća u prvobitni položaj nakon određenih radnji, slično kao kada trajektoid završi jedan pun obrt i vrati svoju orijentaciju nakon što prođe dva perioda puta.
Nauka o izradi prilagodljivih trajektoida je takođe povezana sa drugim naizgled nepovezanim poljem – dijagnozom bolesti putem MRI. „Spin“ je osnovno svojstvo čestica poput protona, koji čine atome vodonika u našim telima. Protoni se ponašaju kao sićušni magneti, čiji „spin“ diktira orijentaciju njihovog magnetnog „severa“. Ovo svojstvo je ključno za mašine za snimanje magnetnom rezonancom (MRI) koje se koriste u bolnicama za skeniranje pacijenata.
Da biste ovo povezali sa Blohovom sferom, uzmite u obzir da svaka tačka i orijentacija na Blohvoj sferi predstavljaju jedinstveno stanje spina protona, slično orijentaciji našeg trajektoida. MRI mašine koriste moćna magnetna polja da poravnaju ove protonske magnete unutar tela u jednom pravcu. Nakon toga, koriste radio talase da poremete ovo poravnanje. Kako se protoni prirodno poravnavaju, oni emituju signale koji se mogu meriti i koristiti za kreiranje detaljnih unutrašnjih slika.
Razumevanje kako se svaki proton vraća na svoju prvobitnu tačku na Bloh sferi pomaže naučnicima da razlikuju ljudska tkiva i identifikuju abnormalnosti. Matematički, stanje spina protona je analogno orijentaciji trajektoida, radio-talasi predstavljaju putanju, a promene u spinu protona izazvane radio-talasima su ekvivalentne kotrljajućem kretanju trajektoida duž putanje.
Matematika koja stoji iza trajectoidnog algoritma otkriva kako se bilo koji dati puls radio talasa MRI može fino podesiti, tako da ponavljanje impulsa dvaput uzastopno vraća sve protonske spinove u prvobitno stanje. Ovaj uvid bi potencijalno mogao poboljšati MRI mašine i poboljšati dijagnozu bolesti sa većom preciznošću.