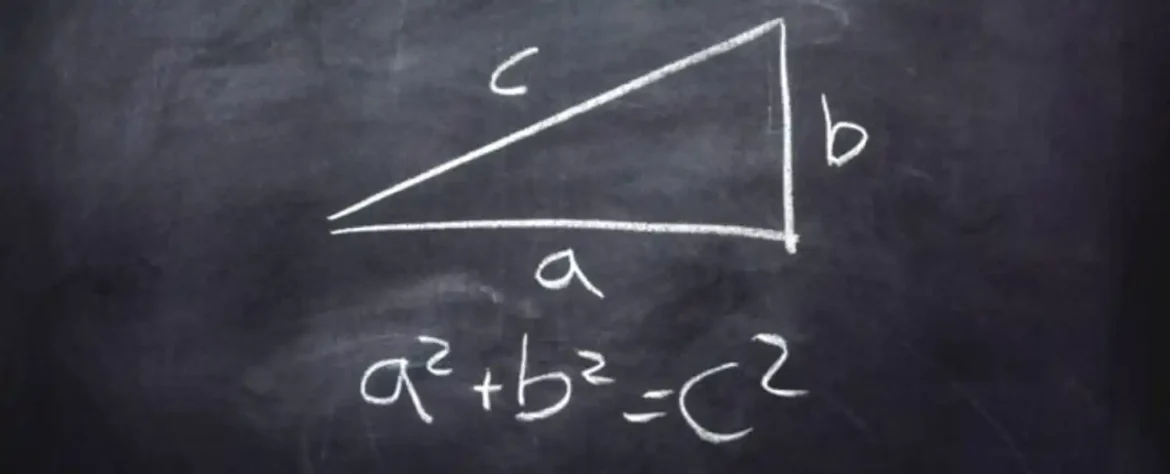U zapanjujućem otkriću, dve srednjoškolke iz SAD, Ne’Kiia Jackson i Calcea Johnson, tokom svoje poslednje godine srednje škole razvile su deset novih dokaza za drevno pravilo Pitagorine teoreme. Ovo istraživanje, koje je započelo kao bonus pitanje na takmičenju iz matematike, dovelo je do novih uvida u ovu ključnu teoremu.
Dugo se smatralo da je korišćenje trigonometrije za dokazivanje Pitagorine teoreme nemoguće zbog kružnog razmišljanja, jer su sve osnovne formule trigonometrije osnova teoreme. Matematičar Eliša Lumis je 1927. godine napisao da „ne postoje trigonometrijski dokazi jer su sve osnove trigonometrije same zasnovane na istinitosti Pitagorine teoreme“.
Međutim, Džekson i Džonson su uspeli da zaobiđu ovu prepreku razdvajanjem različitih verzija trigonometrije i koristeći Zakon sinusa. „Bilo je mnogo puta kada smo obojica želeli da odustanemo od ovog projekta, ali smo odlučili da istrajemo“, pišu autorke u svom radu.
Pitagorina teorema, koja opisuje odnos između stranica pravouglog trougla, je od vitalnog značaja u inženjeringu i građevinarstvu i koristi se vekovima, čak se veruje da je korišćena u izgradnji Stounhendža. U osnovi, teorema se može sažeti u formulu a2+b2=c2a^2 + b^2 = c^2.
„Učenici možda ne razumeju da postoje dve konkurentske verzije trigonometrije koje se koriste istom terminologijom“, objašnjavaju Džekson i Džonson. Razdvajanjem ovih varijacija, uspjeli su da pronađu nova rešenja.
Njihov rad uključuje dokazivanje Pitagorine teoreme za pravougle trouglove sa jednakim stranicama, kao i za one sa nejednakim stranicama. Oni takođe pozivaju na dalja istraživanja, ostavljajući čitaocima prostora da sami otkriju još dokaza.
Matematičar Alvaro Lozano-Robledo sa Univerziteta Konektikat komentarisao je: „Izgleda kao ništa što sam ikada video“. Dela Dumbaugh, glavni urednik časopisa u kojem su objavljeni rezultati, naglašava značaj mladih istraživača u ovom polju.
Džekson trenutno studira farmaciju, dok Džonson nastavlja sa studijama inženjerstva zaštite životne sredine. Njihova dostignuća predstavljaju novu perspektivu u matematici i inspirišu druge mlade istraživače da istražuju složene teme.